Note on Hyperbolic Geometry

Reference Notes

• 2018 Lec Note

• 2015 Lecture note

• Ch5-3 Measurement in Hyperbolic Geometry
• Cheatsheet / Note

Motivation

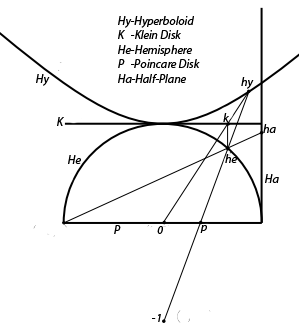
Hyperbolic geometry is a great source of inspiration for math art. Besides it is used to model some hierarchical data structure. Here I collected a few models

Metric

In the Hyperbolic Upper Plane model the metric is simply \(ds^2={1\over y^2} (dx^2+dy^2)\) For the disk model, it’s confined in the unit disk $|z|<1$. \(ds^2=\frac{4(dx^2+dy^2)}{(1-x^2-y^2)^2}=(\frac{2 \|dz\|}{1-\|z\|^2})^2\)

Isometry Transform

We understand our Euclidean space well because we know the isometry of it is translation + rotation (+Mirror) forming the Euclidean group. Note these transforms in Euclidean space is also conformal, making the angles between lines invariant.

For hyperbolic space, knowing the isometry will largely simplify our problem.

Mobius Transform

Mobius transform is a rational function on complex plane, in fact on Riemann sphere.
\(f(z)=\frac{az+b}{cz+d}\) Geometrically it’s the composition of translation, rotation, scaling and inversion (complex inversion). Since it’s analytical complex function, it defines a conformal map!

All the transformations form a group. This group is homomorphic to the matrix group $SL(2,\mathbb C)$ by forming the 2 by 2 matrix s.t. $\det\neq0$ \(\frac{az+b}{cz+d}\mapsto\begin{bmatrix}a&b\\c&d\end{bmatrix}\) This makes it super easy to compute the composition and inversion of any mobius transform.

All the transformations discussed below are subgroups of this class!

Isometry in Poincare Disk

The subset of mobius transform that will make $S^1\to S^1$ are \(\phi:z\mapsto w,\phi(z;a,\theta)=\frac{z-a}{1-\bar a z}e^{i\theta}\) Note this is a complex analytical function, so it’s automatically conformal. Besides its derivative or Jacobian of this map reads \(\frac{\partial w}{\partial z}=\frac{(1-\bar a z)+\bar a(z-a)}{(1-\bar a z)^2}e^{i\theta}=\frac{(1-|a|^2)}{(1-\bar a z)^2}e^{i\theta}\) Through this we could also derive the transformation of metric, showing that it’s isometric \(ds^2|_w=\frac{4 \|dw\|^2}{(1-\|w\|^2)^2}\\=(\frac{\partial w}{\partial z})^2\frac{4\|dz\|^2}{(1-\|\frac{z-a}{1-\bar a z}\|^2)^2}\\=\|\frac{(1-\|a\|^2)}{(1-\bar a z)^2}\|^2\frac{4\|1-\bar a z\|^2\|dz\|^2}{(\|1-\bar a z\|^2-\|z-a\|^2)^2}\\ =\frac{4(1-\|a\|^2)^2\|dz\|^2}{(1-\|a\|^2-\|z\|^2+\|a\|^2\|z\|^2)^2}=\frac{4 \|dz\|^2}{(1-\|z\|^2)^2}=ds^2|_z\) So this transform makes it easy to manipulate shapes in hyperbolic plate.

Isometry in Poincare Half Plane

$a,b,c,d$ real will give the isometry group of Poincare half plane. $PSL(R,2)$

Note the

Connection of 2 models

The 2 models’ metric are connected by Cayley transform. This is a conformal isometry between the 2 models! Note it’s a general mobius transform. \(C:H\to \mathbb D, z\mapsto \frac{z-i}{z+i}\)

Thus all the operations derived for disk or for half plane could be push to the other domain through this link.

Geometric Operations

Poincare disk

The distance from origin to point $z=t\in\R$ is a simple line integration \(d(t)=\int^t_0 \frac{2 dt}{1-t^2}dt = ln(\frac{1+t}{1-t})\) Using this neat formula and the isometric group, we can compute distance between any pair of points. For example, given $z_1,z_2$ we want to map $0\mapsto z_1,t\in\R\mapsto z_2$ and back. Then we know $d(z_1,z_2)=d(t)$.

First consider the forward transform $\phi(t;a,\theta)=z_2$

Here is how to solve $t$ given $(z_1,z_2)$. The core equation is \(a=-z_1e^{-i\theta}\\ z_2=\frac{z_1+te^{i\theta}}{1+te^{i\theta}\bar z_1}\\ e^{i\theta}t=\frac{z_2-z_1}{1-z_2\bar z_1}\) Thus we can solve $t$ from $(z_1,z_2)$.

Note a by-product of this derivation is, given $z_1,e^{i\theta}$ then we can compute $z_2(t)$ i.e. the trajectory of geodesic! Moreover, we can find the tangent vector of geodesic at $z_1$ is $e^{i\theta}$. Thus, it’s surprisingly easy to select a point, and a initial velocity, and then let it travel along the geodesic, just like in Euclidean space. This is a super useful equation for drawing in poincare plane.

Besides, this give us a uniform way to compute the tangent vector along a geodesic connecting $(z_1,z_2)$.

Polygon and Tessellation

Drawing a polygon is not hard, as we have got formula for geodesic connecting any 2 points. But making a regular tessellation is more tricky.

Tessellation in regular space is parametrized by 2 key parameters $p$ the number of edge in one polygon, and $q$ the number of edge joining each other in each vertex.

For Euclidean space, the 2 are linked together, since any polygon has a fixed sum of outer angle $2\pi$, so the inner angle for a $p$ equilateral polygon is fixed. e.g. square tessellation, $p=4,q=4$, hexagon tessellation $p=6,q=3$ etc.

For hyperbolic and spherical space, the 2 are loosely connected, since the sum of inner / outer angle of a polygon depends on its scale.

For example, for a $p$ polygon, we can compute half of one inner angle easily! Assume the first vertex is $D\in\R$ the neighboring vertex will be $De^{i{2\pi/p}}$. Then the initial tangent of edge curve is \(e^{i\theta}t=\frac{D(e^{i{2\pi/p}}-1)}{1-e^{i{2\pi/p}}D^2}\\ \theta= ang(\frac{e^{i{2\pi/p}}-1}{1-e^{i{2\pi/p}}D^2})\) Another constraint is there are $q$ inner angle at each joint, so \({2\pi\over q}=\pi-ang(\frac{e^{i{2\pi/p}}-1}{1-e^{i{2\pi/p}}D^2})\) This could be numerically solved instantaneously, since the right hand side is a monotonic function of $D$. Using this formula, we could easily draw a equilateral polygon that is able to tessellate the plate!

Mobius Group Action

For tessellation, we also have to derive the mobius transform and make it act on the polygon recursively!

The final results look like this.

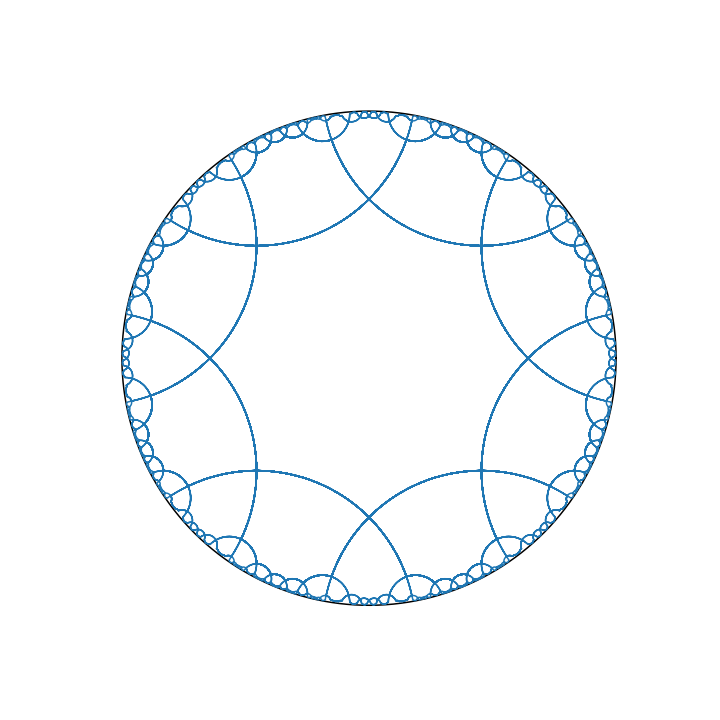
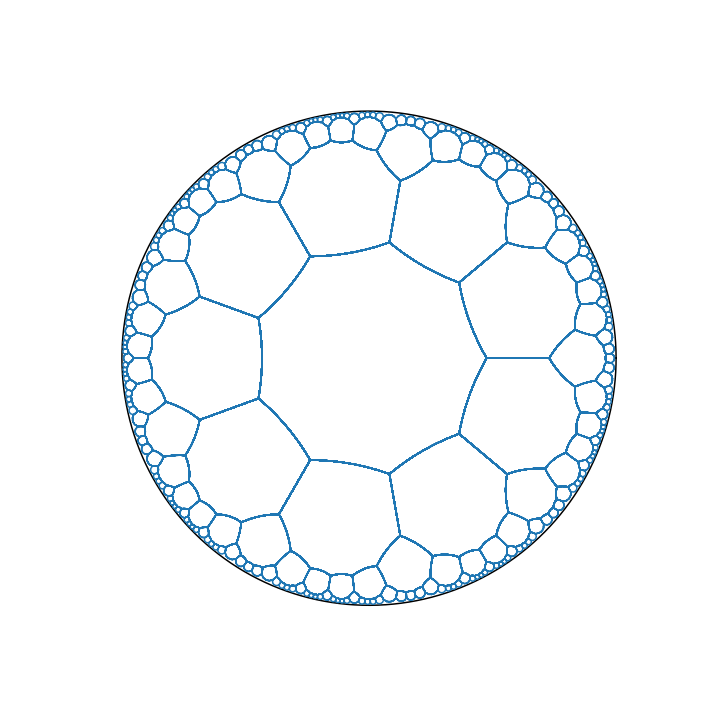
Source codes are deposited in this repo as a notebook.