Motivation

This is a brief analytical note about how physical self movement of eye / camera will induce optic flow in a static environment. And then discuss how a system can separate these two components instantaneously.

The major reference is 1981 The interpretation of a moving retinal image.

Derivation

Given a physical world coordinates \(p=(X,Y,Z)\;\\ \bar p=(x,y,1)=(X/Z,Y/Z,1)\) And the camera movement in the real world coordinate, Rotation vector $W=[w_x,w_y,w_z]$ and translation speed $V=[v_x,v_y,v_z]$. The effective movement of position of object point is \(\dot p=-V-W\times p\\ \dot X=-v_x-w_y Z+w_z Y\\ \dot Y=-v_y-w_z X+w_x Z\\ \dot Z=-v_z-w_x Y+w_y X\) Thus the apparent visual movement could be derived \(\dot x =\dot X/Z-X\dot Z/Z^2\\ \dot y =\dot Y/Z-Y\dot Z/Z^2\\ \dot x =-v_x/Z-w_y+w_z y+v_z x/Z+w_x xy-w_y x^2\\ \dot y =-v_y/Z-w_z x+w_x+v_z y/Z+w_x y^2-w_y xy\\\) Thus, a translational and rotational components could be separate out \(\dot x^T=(-v_x+v_z x)/Z\\ \dot y^T=(-v_y+v_z y)/Z\\ \dot x^R=-w_y+w_z y+w_x xy-w_y x^2\\ \dot y^R=-w_z x+w_x+w_x y^2-w_y xy\) Note the translation velocity vector $V=[v_x,x_y,v_z]$ can be seen as the homogeneous coordinate of the vanishing point or epipole. Using this coordinate of epipole, $e=(e_x,e_y,1)=(v_x/v_z,v_y/v_z,1)=\bar V$ then the translational optical flow could be written as \(\dot x^T=(x-e_x){v_z\over Z}\\ \dot y^T=(y-e_y){v_z\over Z}\) Thus it shows that

• all the optical flow induced by translation are along the epipolar line direction $[x-e_x,y-e_y]$,
• Expansion is caused by positive $v_z$ , Convergence is caused by negative $v_z$
• This will give rise to the so called VZ ratio, which is similar to depth or disparity in stereo vision.

Flow Attribution

Using the geometric property above, we can compute the parameters of $V,W$ by fitting them through RANSAC

1981 The interpretation of a moving retinal image.

Epipolar Geometry

Fundamentally, epipolar geometry is about how points coordinate looks differently from different perspective.

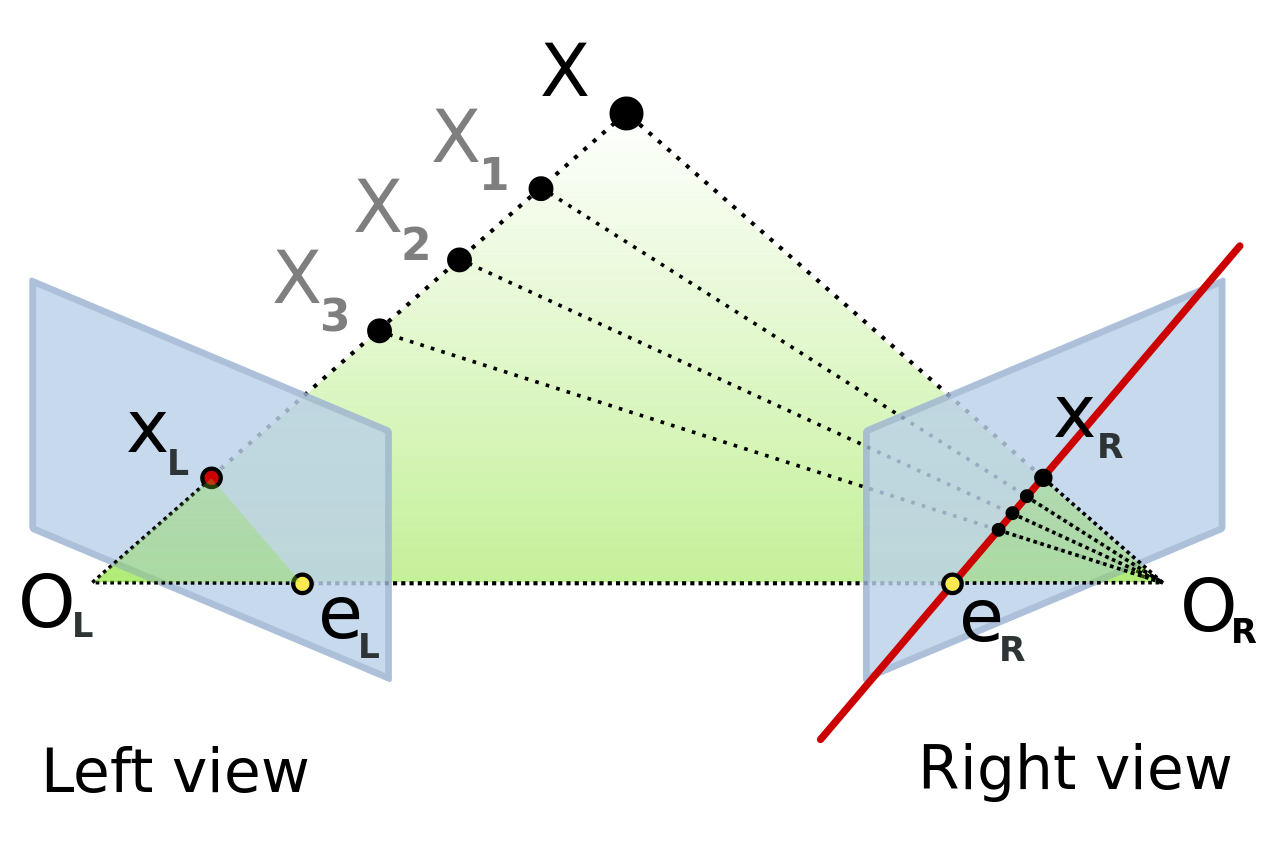
The beginning of epipolar geometry is,

Given 2 pinhole cameras, for a given point in view 1, the corresponding point in view 2 must lie on a line defined by geometry.

The rank 2 foundamental matrix is a way to formalize this.