引言: 感觉系统

一直以来我都被这个简单的事实深深震撼: 我们的心智(mind)其实一直都生活在一个密不透风, 不见天日的黑匣子里(Skull), 但因为我们无比强大的感觉系统(Sensory System), 我们才能在神经信息处理的过程中渲染出这样清晰美妙的主观现实, 并无缝的与这个世界交互. 感觉系统就是这个探测外在物理环境转换成主观现实的存在呀. 1

在科学还属于哲学的时代, 人们就知道人的感觉至少是有5种主要模态(modality)的, 视觉, 听觉, 嗅觉, 味觉, 触觉(包括痛觉,痒).2 对于任何一种感觉模态, 神经系统核心的问题都是, 如何快速(fast), 有效(efficient)的表征(represent), 分析(analyze)物理世界的刺激, 得到有用的信息. 类似于对电路的分析, 神经环路的分析(neural circuit analysis), 就在追问神经元自身性质(被其中的分子机器决定), 及其连在一起组成的环路是如何解决上述信号处理中的”工程计算”问题的.

作为一个例子, 这篇post要科普的就是不同生物(特别是低等生物) 的听觉感受细胞是如何解决频率选择问题的.

问题: 频率选择(Frequency Tuning)

就像我们每天听到的乐音, 任何听觉刺激的一个主要属性就是其频率. 因而神经系统想要表征声音信号的一种策略就是去表征声音里的不同频率成分的强度. 事实上, 生物系统似乎的确采取了这种表征策略: 以纯音信号去刺激, 耳蜗的神经节细胞(Cochlea Ganglion Cell), 到听皮层的细胞都拥有一定的频率选择性(frequency tuning). 那么对声音频率的选择性是怎么通过耳朵里的生物结构实现的就是一个有趣的问题.

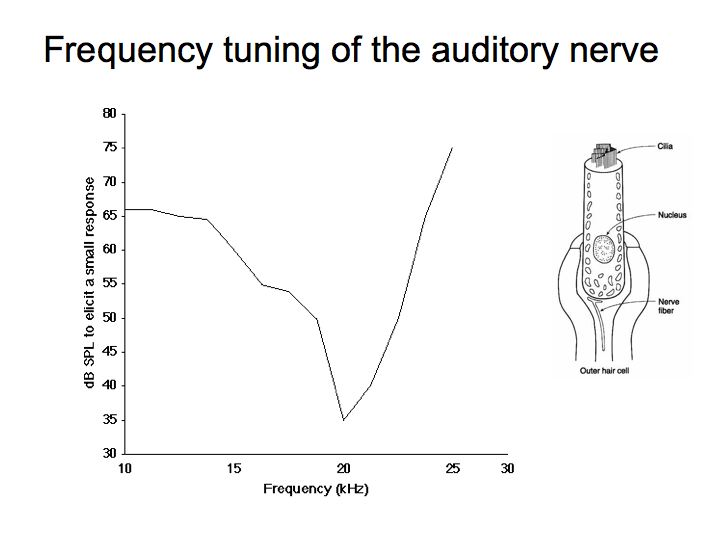
(下图是一根听神经对输入频率的选择性. 通过测量不同频率诱发微小响应的声音阈限来展示. )

Frequency Tuning

生物框架: 听觉系统与听毛细胞(Hair Cell)

为了能欣赏生物系统的解决方案, 首先对要听觉系统的结构做一个快速介绍.

以人为例, 声波会先通过外耳耳道, 将震动传递至鼓膜, 在中耳的听小骨处, 机械波转变为听小骨的连锁震动, 并敲击内耳的耳蜗卵圆窗 (oval window).

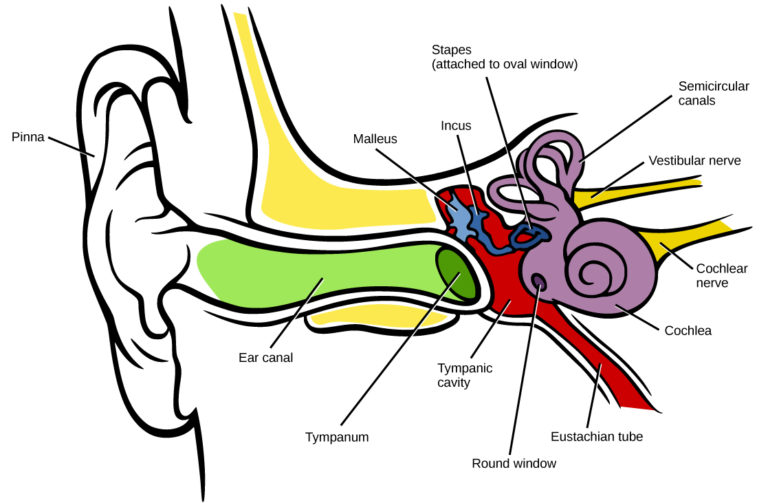
Ear structure and cochlea

卵圆窗是耳蜗中一条充满淋巴液体的管道的端口, 因此敲击这一端就像敲击一个充满水的弹性管子, 会引起管壁的震动. 这里, 震动的管壁就是基底膜(Basiliar Membrane/fiber), Cochlea Overview

从下图中容易看到, 基底膜的震动会带动其上纤毛的震动(就是hair cell头上的那一撮毛”hair”), 导致纤毛簇的弯折. 而纤毛簇的弯折又会通过一些毛端连接(tip link)引起一些精巧设计的机械控制离子通道的打开, K+离子涌入导致细胞膜电位的升高(depolarization), 最终将震动的机械信号转换成电流幅度信号, 通过与听神经(auditory nerve)的突触连接, 传输给神经系统. Hair Cell and Basiliar Membrane

那么这个系统是怎么让不同的听毛细胞产生不同的频率选择性的呢?

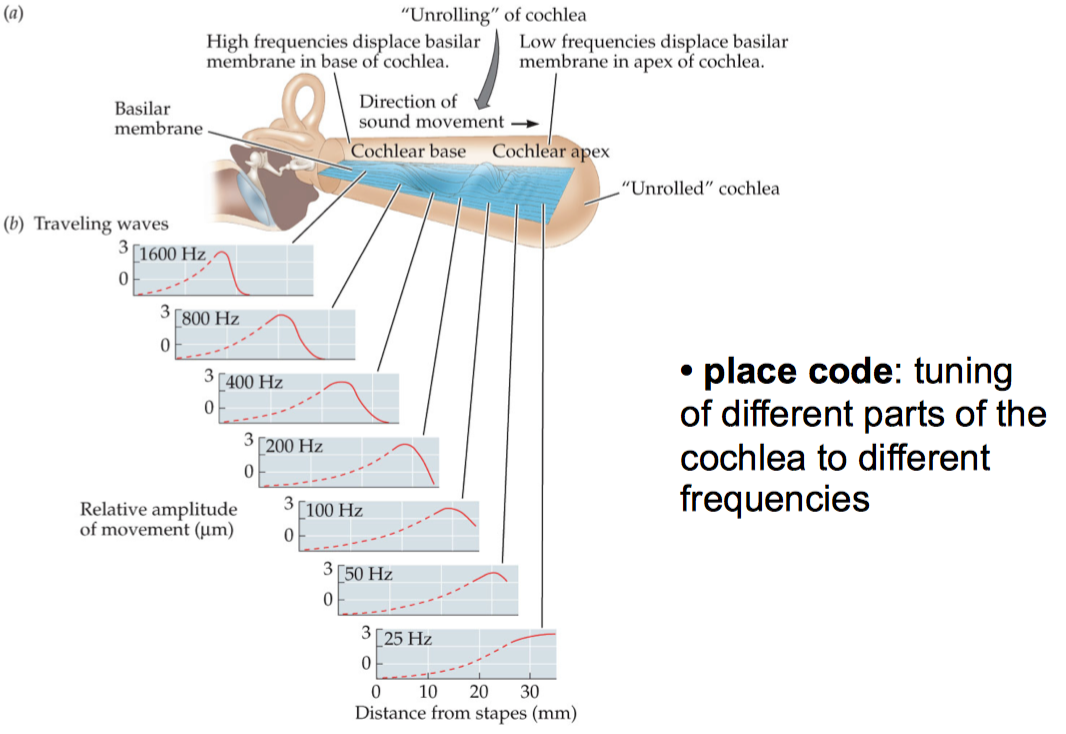
对于很多高等动物, 其耳蜗基底膜有着独特的力学属性, 靠近底端的基底膜较硬, 刚性很大, 顶端较宽较软. 可以类比机械共振来理解, 基底膜的底端在高频振动输入下震动响应很强, 而顶端在低频震动输入下震动响应很强. 最佳刺激频率随基底膜上的位置连续变化, 从而当不同频率的听觉刺激输入, 其会激起不同位置的最强震动, 因而响应的听毛细胞, 听纤维也完全不同. 这就是所谓听觉系统的位置编码(Place Code),2 换言之是通过耳蜗与基底膜的机械力学属性达成的频率选择. 3 Place_Code

然而问题来了, 对于许多并没有很长的耳蜗基底膜(Cochlear Basal Membrane)的生物, (如乌龟, 小鸡, 青蛙), 他们的耳蜗机械力学属性并不独特, 无法帮助他们完成频率选择, 那怎样才能解决这个问题呢? (如下图的牛蛙, 便是下文中诸多研究的对象, 箭头指向其耳朵)

Frog_ear

低等动物的精妙解答(Elegant Solution in Lower Vertebrate)

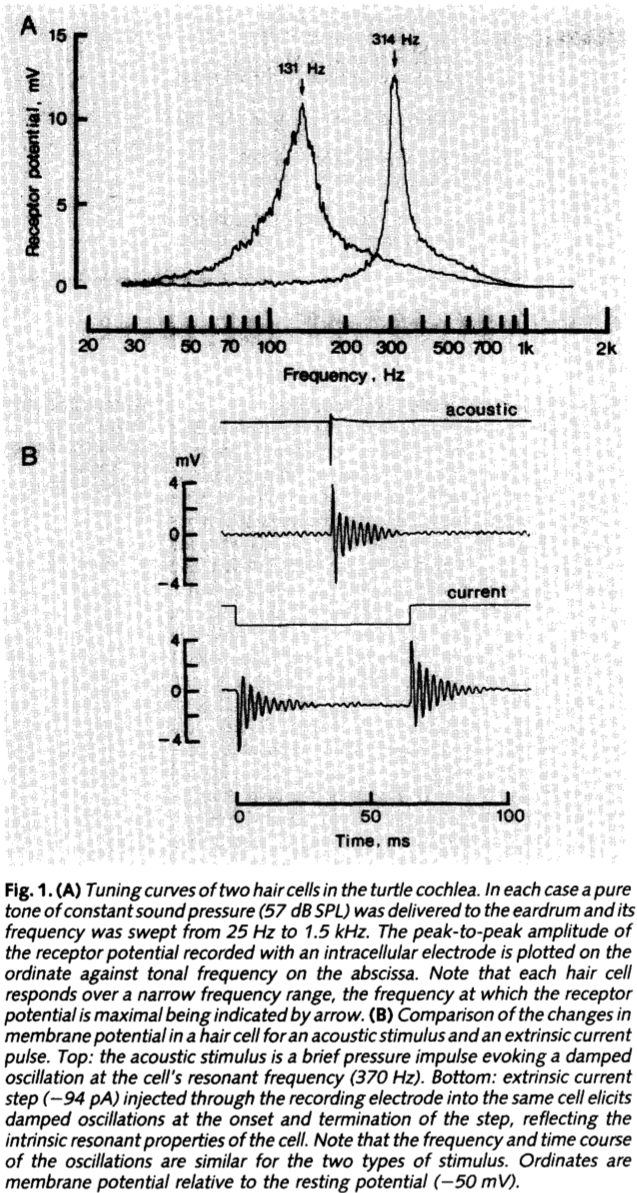
让我们一点点揭开答案, 首先从这张测量开始4. 这幅图来源于乌龟耳蜗中听毛细胞的电属性测量. 上图展示了不同频率声音刺激毛细胞, 得到的膜电位振幅曲线, 一条如电学系统般漂亮的频选曲线(tuning curve). 下图展示了用一个声音脉冲, 或者是电流方波去刺激听毛细胞, 都会诱发膜电位的衰减震荡(damped oscillation). 那么对输入频率的选择性, 与对刺激的衰减震荡响应, 这两种现象之间有什么联系呢?

Exp_data_1

看到这么漂亮的曲线, 自然会想去建模. 输入电流, 输出电压, 衰减, 震荡, 频率选择, 这几个关键词放在一起, 是否让你想起了什么悠远的记忆呢? (比如大一学过的大学物理/电磁学? ) 对的, RLC震荡电路. 5

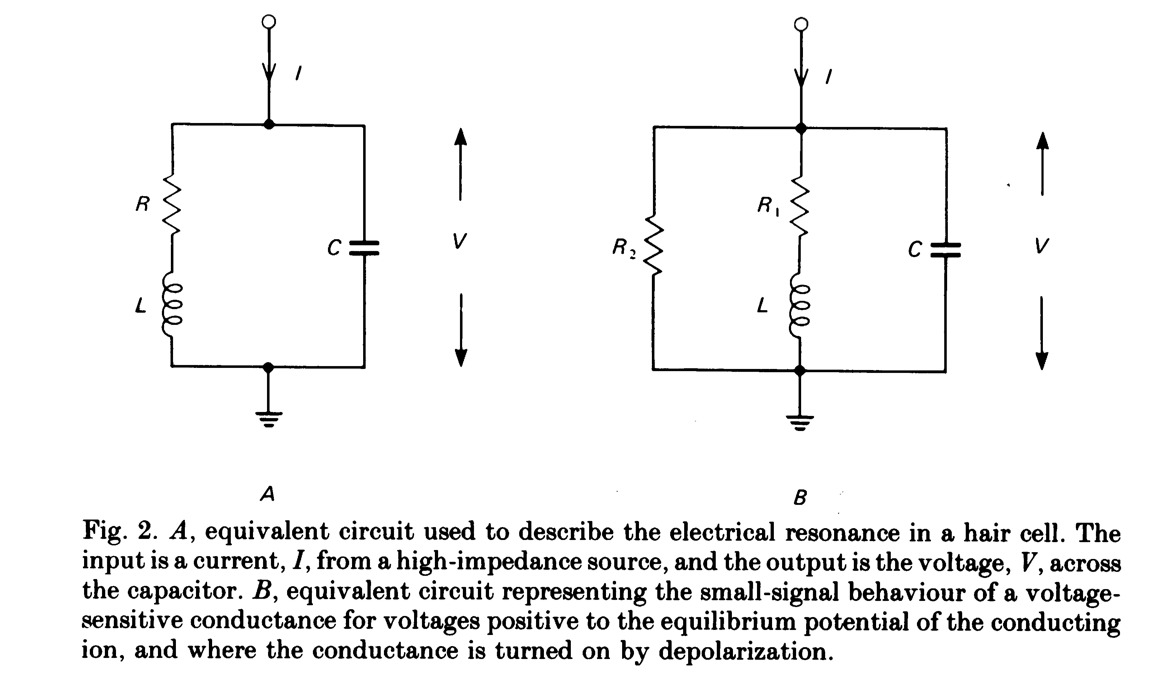
Model_1

以微分方程的形式描述电路就是

\[V = RI_1 + L\dot {I_1} \\ C\dot V + I_1 = I\]

消元得到

\[V = R(I-C \dot V) + L(\dot I - C\ddot V)\]

稍加整理就可以得到标准的外界驱动下的衰减震荡方程. ($\gamma = R/L,\ \omega_0^2=1/LC$)

\[\ddot{V}+\gamma \dot{V}+\omega_0^2 V = \gamma \frac{I}{C} + \frac{\dot I}{C}\]

有了这一简洁的模型系统, 可以解析的分析其在不同输入条件下的行为.

该系统在正弦波电流$I=\bar{I}\sin(\omega t)$输入下的解, 抛去暂态项, 稳态解为$\boldsymbol{V}=A(\omega)\sin(\omega t+\phi(\omega))$, 其中

\[A(\omega)=\frac{\overline{I}}{\omega_{0}C}\left\{\frac{Q^{2}+\omega_{0}^{2}/\omega^{2}}{\left(\frac{\omega}{\omega_{0}}-\frac{\omega_{0}}{\omega}\right)^{2}Q^{2}+1}\right\}^{\frac{1}{2}}\\ \phi(\omega)=\tan^{-1}\left\{\frac{\omega Q}{\omega_{0}}-\frac{\omega^{3}Q}{\omega_{0}^{3}}-\frac{\omega}{\omega_{0}Q}\right\}\]

很容易看出电压震荡幅度与输入频率有一个选择峰(Tuning peak).

再去求解该系统在方波电流$I=\bar{I}u(t)$输入下的解, 容易得到

\[V_{u}=\overline{I}R\left\{1+\frac{\omega_{0}^{2}}{\omega_{f}\gamma}e^{-\gamma t/2}\sin\left(\omega_{f}t-\phi^{\prime}\right)\right\}\\ \phi^{\prime}=\sin^{-1}\frac{\omega_{f}\gamma}{\omega_{0}^{2}}\]

可以发现, 这一模型非常好的复刻了电生理测到的衰减震荡行为, 同时也解释了对输入频率的选择性, 他们是一体两面, 完美! 但是, Caveat! 需要注意, 仅凭方程的形式并不能判定这个系统是按照上图的电学模型运作的! 甚至, 我们都不知道这个系统是一个电学系统还是一个等效的力学系统—用弹簧, 质量与阻尼同样可以得到同样的方程. (就像高等脊椎动物的听毛就是机械力学选频系统). 而且即使是电学系统, 与上述动力学等效的通道、化学机制动力学机制也数不胜数.

因而唯象模型建到这一步已经完美了, 要进一步确认其机制, 就要做进一步的电生理实验, 控制, 扰动, 拆解(control, perturb, dissociate)这一系统.

在上述唯象描述的文章5发表几年后, 进一步解析其生物机制的两篇背靠背文章6,7, 也出现了. 我们先根据先前的模型来猜测下可能的生物机制是怎样的.

如果要产生一个衰减震荡, 必要的条件就是回复力(rebounding force), 或者说反馈, 无论是力学的回复, 还是电学的回复. 在这里我们先假设震荡是电学震荡, 也即回复是由电属性提供的. 而上图中的电流输入刺激, 或是声音脉冲刺激, 都是直接改变膜电位$V$的, 8. 既然这两种刺激都能开启震荡, 那一种可能性就是存在电压依赖的离子通道(Voltage Gated Ion Channel), 提供一个电流$I_{g(V)}=g(V)(V-E)$, 而该电流可以进一步改变电压, 构成一个动力系统~

\[C\frac{dV}{dt}=-g(V)(V-E)-g_L(V-E_L)+I\]

然而众所周知, 1维动力系统无法构成震荡, 必然还有些动力学变量, 或者是$g(V)$的电压依赖并非瞬时的, 而有些许延迟, 或者还有其他通道涉及其中. 这时, 纯粹理论的推断就无法前进了, 必须依据生物体内具体的通道类型进行推断.

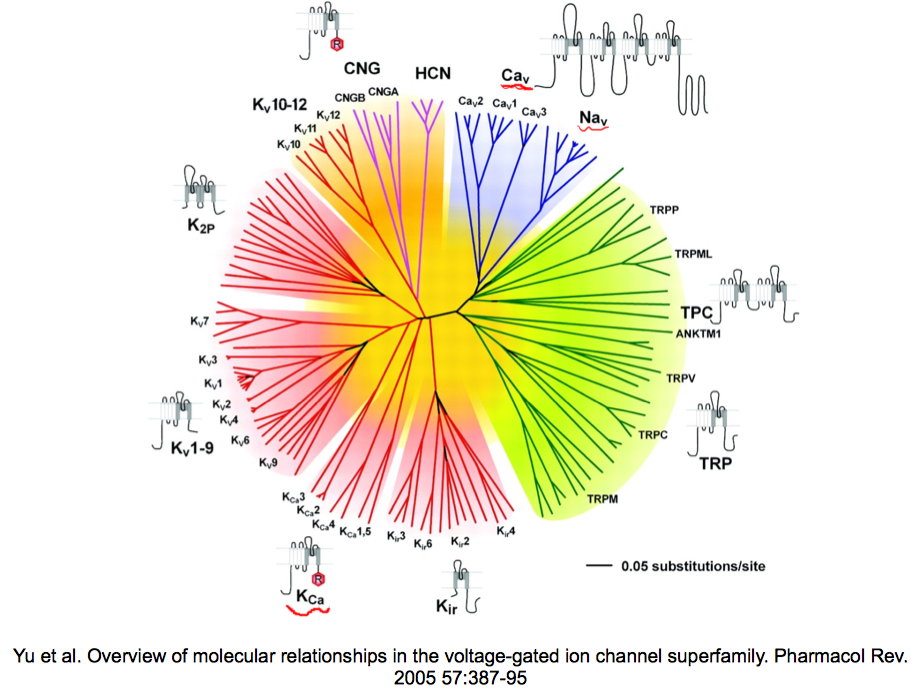
Channel Variety

而当时的人们有充足的药物, 化学手段做到这一点. 通过施加药物, 可以选择性的堵塞, 关闭某些离子通道; 或者可以调整溶液离子浓度, 从而判断出哪些离子涉及该反应. 上图是神经元上各类离子通道类型的一幅总括, 在这一Big Picture中, 划红线的$Ca_V,K_{Ca}$, 即电压依赖的钙通道与钙依赖的钾通道涉及这一过程. 非常有趣的是这两种通道的关系正应了前面动力系统分析的推测—存在一种依赖于电压的通道$Ca_V$, 同时另一种通道$K_{Ca}$与之耦合.

明确了通道及其属性, 机制也就清晰起来, 膜电位$V$的升高诱发$g_{Ca_V}$通道打开, 然后$Ca^{2+}$离子的涌入打开了依赖于$Ca^{2+}$的$K^+$通道, 使得$K^+$涌出, 降低膜电位, 关闭 $g_{Ca_V}$通道. 不过这样仅完成了一个回合, 还无法震荡, $Ca^{2+}$的浓度会通过扩散慢慢降低(类似一种适应adaptation机制), 从而关闭$g_{Ca_V}$, 回复膜电位. 这样整个系统就周而复始的运转起来, 产生震荡.

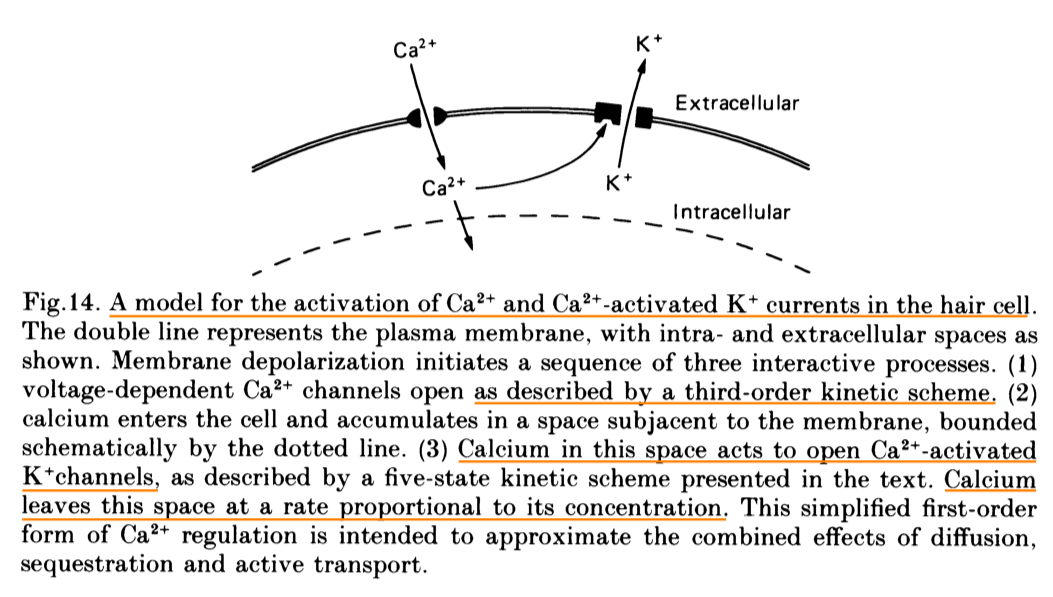
Mechanistic Model

进一步研究发现, 可以通过调节模型中的$g_{K_{Ca}}$通道的密度, 改变震荡频率与衰减频率, 换言之, 只要连续改变不同细胞内的$K_{Ca}$通道的蛋白表达量, 即可得到对输入信号在空间上的频率分解了!!

在知道谜底时, 我对进化的足智多谋(resourceful)佩服得五体投地—用不了机械工程(Mechanical Engineering)的办法, 就用生化电生理(Biochem/Electrical engineering)的办法来解决频率选择问题!

事实上, 在感知觉系统中, 不同生物都面临着相似的”工程”问题的挑战, 而就像其他工程问题一样, 问题总有许多的解决方案, 但最终选择哪一种, 依赖于许多物质条件的限制, 而不只是最优性. 而在一些更低等动物简单的狭小的神经系统中, 我们更会被那些有限资源下令人惊艳的”设计”所震撼, 比如这个故事中的”设计”—-采用两个相互耦合的离子通道(电压依赖Ca2+通道与Ca+ 依赖的K+通道) 组成震荡的动力系统已然让人惊叹; 而用细胞内在的震荡频率(intrinsic frequency)作为对输入频率的选频器更是让人击节称叹; 在这个设计下, 不同细胞里不同的通道的表达量(expression level), 即可调节通道密度(channel density)这个参数来调节动力系统的内在震荡频率, 从而组成空间分频阵列, 形成Frequency Place Code. 只能说, 如果让我解决这个工程问题, 我有限的知识与智力一定想不出这么简洁优美的办法, 在生物系统中实现.

听毛细胞震荡的数学模型

(如果您对数学模型一点没有兴趣, 这一部分可以直接跳过! 但如果像一些读文章喜欢直接看图看公式的人, 或是对计算神经/生物模型有过一点了解, 或者对这篇文章的主题有学术兴趣的人, 这一部分就是为您准备的~)

那么这个机制性的计算模型是如何搭建的呢? 具体的若要写成方程组就是, 膜电压方程:

\[C\frac{dV}{dt}=-I_{Ca}-g_{K_{Ca}}(V-E_K)-g_L(V-E_L)\]

类似Hodgkin, Huxley在巨型乌贼上研究动作电位时开发的模型, 这里的电压依赖钙电流也可以写成类似的形式: 电流3次依赖于门控变量$m$, $m$以一阶动力学依赖于电压决定的平衡值与时间常数. 其中流入的Ca电流是

\[I_{Ca}=\bar{g_{Ca}} m(t)^3 (V-E_{Ca})\]

门控变量的动力学为

\[dm/dt = \beta_m (1-m) -\alpha_m m\\ \alpha_{m}=\alpha_{0}\exp\left[-\left(V_{\mathrm{m}}+V_{0}\right)/V_{\mathrm{A}}\right]+K_{\mathrm{A}}\\ \beta_{m}=\beta_{0}\exp\left[\left(V_{\mathrm{m}}+V_{0}\right)/V_{\mathrm{B}}\right]+K_{\mathrm{B}}\]

进一步, 靠近细胞膜处钙离子浓度动力学被过膜的钙电流与钙自身的扩散决定,

\[\frac{d[\mathrm{Ca}^{2+}]}{dt}=UI_{Ca}/(zFC_{vol}\xi)-K_{s}[Ca^{2+}]\]

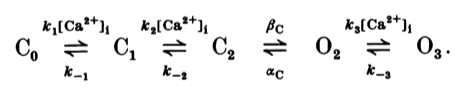
而他们还做了非常精细的单通道电生理测量, 对Ca依赖的K通道采用了5状态转换模型. 钙离子影响K通道的动力学由经典的通道动力学模型决定, Channel_States

具体的微分方程组可以按照上图以质量作用定律如下写出, 作者在论文中还加入了一些解离速率对膜电位的依赖, 此处不再赘述.

\[\mathrm{d}C_{0}/\mathrm{d}t=k_{-1}C_{1}-k_{1}\left[\mathrm{Ca}^{2+}\right]_{\mathrm{i}}C_{\mathrm{o}}\\ \mathrm{d}C_{1}\mathrm{d}t=k_{1}\left[\mathrm{Ca}^{2+}\right]_{\mathrm{i}}C_{0}+k_{-2}C_{2}-\left(k_{-1}+k_{2}\left[\mathrm{Ca}^{2+}\right]_{\mathrm{i}}\right)C_{1}\\ \mathrm{d}C_{2}/\mathrm{d}t=k_{2}\left[\mathrm{Ca}^{2+}\right]_{\mathrm{i}}C_{1}+\alpha_{\mathrm{C}}O_{\mathrm{2}}-\left(k_{-2}+\beta_{\mathrm{C}}\right)C_{\mathrm{z}}\\ \mathrm{d}O_{2}/\mathrm{d}t=\beta_{\mathrm{c}}C_{2}+k_{-3}O_{3}-\left(\alpha_{\mathrm{C}}+k_{3}\left[\mathrm{Ca}^{2+}\right]_{\mathrm{i}}\right)O_{\mathrm{2}}\\ \mathrm{d}O_{3}/\mathrm{d}t=k_{3}\left[\mathrm{Ca}^{2+}\right]_{\mathrm{i}}O_{2}-k_{-3}O_{3}\\\]

而$g_{K_{Ca}}$的开放程度由处于最后两个开放状态$O_2,O_3$的通道数量决定.

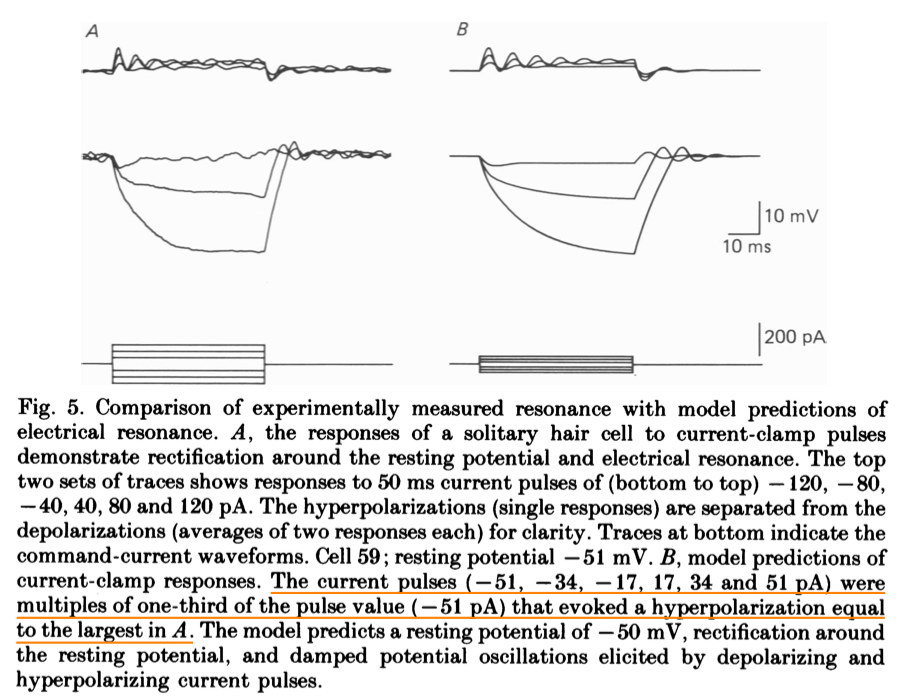
\[g_{K_{Ca}}=\overline{g}_{K_{Ca}}(O_{2}+O_{3})\]

这样, 整个系统作为一个巨大的常微分方程组(ODE)就闭环了! 通过许多电生理实验确定相应参数后, 用计算机模拟这个模型, 可以得到与实验测量定性相仿的电压震荡曲线, 如下图所示, 定性模拟得很好! 而且改变实验条件(如$Ca^{2+}$浓度, 施加药物堵塞通道), 测量到的震荡频率变化曲线, 也可用模型参数变化导致的频率变化曲线来极好的拟合. 可以说是一个极其成功的生物物理模型了.

Model Validation

后记

这个故事是在最近的Cell Neurobiology课上听到, 当场就被惊艳到, 并决定写个post督促自己学习下. 查了文章才发现, 这一系列的实验、模型工作是30年前的, 大致在1980-1990左右完成9, 完全可以想见那时人们第一次看到细胞膜上能记录到如电路般漂亮的震荡电压时的震撼与惊喜.

从这个故事可以得到这样几个有益的教训(lesson):

  1. 基于很好的单细胞电生理数据, 能做出很棒的唯象模型. 而根据唯象模型可以去猜测推断通道的机制, 进而能做出从机制出发搭建出完整的机制模型(mechanistic model), 再根据模型的预测与测量比对验证. (有时觉得能遇到这样漂亮数据的生物物理学家真的三生有幸. 看到那样干净的电震荡数据, 哪怕是物理系的本科生, 脑子里大概也能立即蹦出几个电路模型来)
  2. 然而要实际验证这些模型的推断则需要pharmacology药物干扰, 确定通道类型; 进行精细的patch clamp实验, 确定电生理参数; 精细的验证不同输入条件下模型的行为(behavior)与细胞一致. 6 最后才能肯定这是一个好模型. 模型是一个开始, 而从不是终结.
    1. 这也会促使我们去想, 现在的System Neuroscience, 特别是对cortex的建模中, 什么样的模型是可能的呢? 什么样的模型是可验证的呢? 恐怕由于参数数量的巨大, 和测量数据的稀疏, 所能做的验证总十分有限, 模型通常的预测能力也就很捉急了.
  3. 不同寻常的模型生物身上, 也许有着很不同的问题解决策略, (文中所说的机制是在乌龟, 小鸡和牛蛙等生物身上得到的). 需要注意, 低等动物的问题解决策略不一定就简单, 反而可能更令人称叹! 高等动物的解决方案也不一定就复杂. (Cf. Sebastian Seoug, 一些高等动物的皮层(Cortex)也许比线虫(C Elegans)和视网膜(Retina)更容易理解)
  4. 硬币的另一面, 这个故事虽然极其美丽, 但可推广性也许比较有限, 应用价值也不一定就很大. (也许可以开发基因疗法帮助你家的乌龟治疗听力损伤?) 不过, 这也是在post里选择讲这个故事的原因: 去展现一些美丽而无用的东西, 而这是科学与自然(Science and Nature)本来的样子.

  1. 这篇post是一系列试图以容易的方式解释Neuroscience的一部分, 大概也是我对自己写作能力的训练了. 写作于Oct.15th-Oct.29th期间. ↩

  2. Narayan, S. S., Temchin, A. N., Recio, A., & Ruggero, M. A. (1998). Frequency tuning of basilar membrane and auditory nerve fibers in the same cochleae. Science (New York, N.Y.), 282(5395), 1882-4. ↩ ↩2

  3. 事实上正是因为耳蜗的位置编码理论, 现代的人工耳蜗植入物(Cochlea Implant)便是将输入声音分解成不同频段成分输送给耳蜗不同位置的听纤维的. 换言之, 是使用电子电路代替耳蜗完成了频率分选的任务. ↩

  4. Fettiplace, Robert. “Electrical tuning of hair cells in the inner ear.” Trends in Neurosciences 10.10 (1987): 421-425. ↩

  5. Crawford, A. C., & Fettiplace, R. (1981). An electrical tuning mechanism in turtle cochlear hair cells. The Journal of Physiology, 312(1), 377-412. (电学唯象模型文章) ↩ ↩2

  6. Hudspeth, A. J., and R. S. Lewis. “Kinetic analysis of voltage‐and ion‐dependent conductances in saccular hair cells of the bull‐frog, Rana catesbeiana.” The Journal of Physiology 400.1 (1988): 237-274. ↩ ↩2

  7. Hudspeth, A. J., & Lewis, R. S. (1988). A model for electrical resonance and frequency tuning in saccular hair cells of the bull‐frog, Rana catesbeiana. The Journal of physiology, 400(1), 275-297. (这两篇背靠背文章加起来有60页也是那个时代研究者的风范了. 两篇文章在超长篇幅里做了极其全面的研究, 从电生理, 药物, 单通道测量到模型, 计算, 理论工作, 十分扎实.) ↩

  8. 当然这个猜测不唯一, 可能是电流输入引发了细胞自身的机械振动, 声音脉冲也引起了机械振动, 是震动开启了膜电位震荡. ↩

  9. 事实上, 那几年有大量关于听毛细胞的基本电生理属性的经典工作被完成. 而这篇科普引用的几篇论文的作者A. James Hudspeth, Robert Fettiplace也刚在2018年获得了Kavli Prize for Neuroscience. 也是很巧了. ↩