The Geometry of Deep Generative Models and Its Applications (ICLR 2021)
This is the project page for the paper The Geometry of Deep Generative Models and Its Applications.
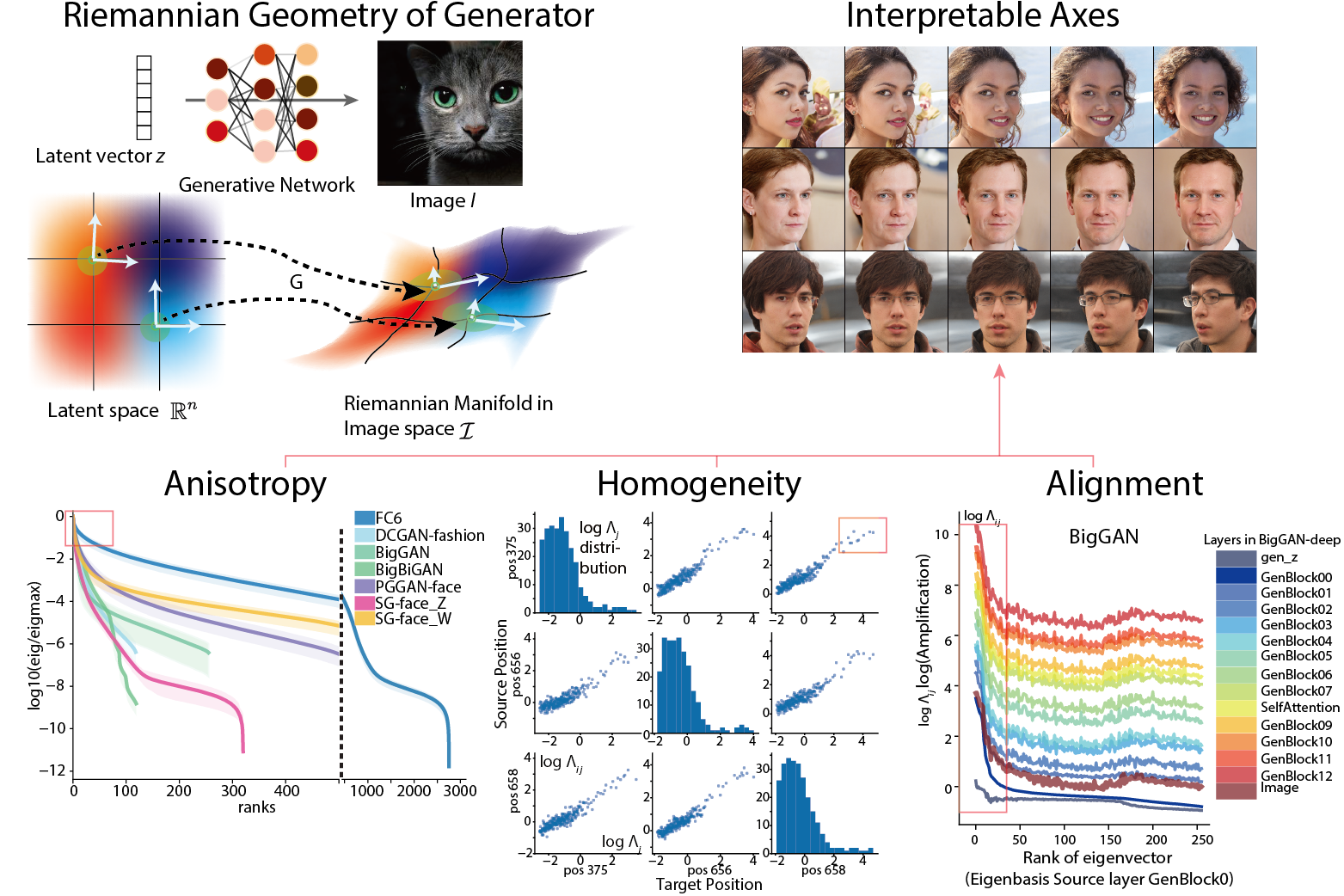
In this work, we explored the structure of the latent space of generative models from a differential geometric perspective. We developed an architecture agnostic tool to efficiently compute Riemannian metric tensors of the manifold created by generators. Surprisingly, analysis of the metric tensor on the manifold of many modern generators showed that they exhibit many common geometric features, i.e. anisotropy among directions, homogeneity in space, and alignment across layers. These geometric properties unifies many previous methods to discover interpretable axes in the space. Leveraging the geometry of the space yields more efficient way to optimize on the image manifold of generators.
This work is accepted in ICLR 2021. Paper: OpenReview; ArXiv
Citing this Work
@inproceedings{
wang2021aGANGeom,
title={A Geometric Analysis of Deep Generative Image Models and Its Applications},
author={Binxu Wang and Carlos R Ponce},
booktitle={International Conference on Learning Representations},
year={2021},
url={https://openreview.net/forum?id=GH7QRzUDdXG}
}